Question

An aircraft carrier traveled to a navigational buoy and back. It took six hours longer to go there than it did to come back. The average speed on the trip there was 10 mph. The average speed on the way back was 22 mph. How many hours did the trip there take?

Answer 1

11 mph

Explanation:

Given that:

Average speed on the trip = 10 mph

Average speed on the way back = 22 mph

Let time taken on the trip to navigational buoy =
`t` hours

As per question statement, Time taken on the way back =
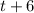`t+6` hours

Formula used:

`Distance = Speed * Time`

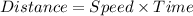
The distance traveled on the way to navigational buoy and the distance traveled on the way back are traveled.

Writing equation:

`22t=10(t+6)\\\Rightarrow 22t=10t+60\\\Rightarrow 22t-10t=60\\\Rightarrow 12t=60\\\Rightarrow t=5\ hours`

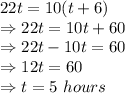
It is given that the time taken in the trip is 6 hours more than that of time taken on the way back.

So, time taken on the trip = 6 + 5 = 11 mph