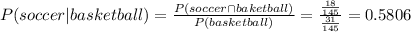Answer:
0.5806
Explanation:
Out of a group of 145 students that were surveyed about sports, 31 said they play basketball and 59 said they play soccer. 18 of the students who said they play basketball said they also play soccer. If a student is chosen at random, find the probability. P (Soccer |Basketball).
Solution:
P(soccer) = number of students playing soccer/ total number of students.
P(soccer) = 59/145
P(basketball) = number of students playing basketball/ total number of students.
P(basketball) = 31/145
P(soccer and basketball) = number of students playing soccer and basketball/ total number of students.
P(soccer and basketball) = 18/145
From Bayes theorem:
P(A | B) = P(A ∩ B) / P(B)
Hence: