Question

Find the roots of:


`1.\ &2x^3-7x^2+8x-3=0\\ 2. \ & x^3-x^2-4=0\\ 3. \ &6x^3+7x^2-9x+2=0 \end{align*}`

Answer 1

`\large\displaystyle\text{$\begin{gathered}\sf \pmb{1) \ 2x^3-7x^2+8x-3=0 } \end{gathered}$}`

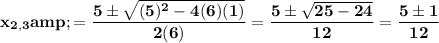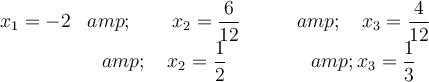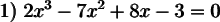
Synthetic division is used since the equation is of the third degree. The divisors of -3 are 1, -1, 3, +3. So:

| 2 -7 8 -3

1 | 2 -5 3

| 2 -5 3 0

1 | 2 -3

2 -3 0

So the factorization is (x-1)² (2x-3)=0. So:

`\bf{ x_1=x_2=1 \qquad x_2=(3)/(2) }`

`\large\displaystyle\text{$\begin{gathered}\sf \pmb{2) \ x^3-x^2-4=0 } \end{gathered}$}`

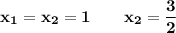
Synthetic division is used since the equation is of the third degree. The divisors of -4 are 1, -1, 2, -2, 4, -4. So:

| 1 -1 0 -4

2 | 2 2

1 2 2 0

So the factorization is (x-2)(x²+x+2)=0 . When calculating the discriminant of the trinomial, it is concluded that it has no roots since the result is negative. So you only have one solution.

`\bf{ 1^2-4(2)(2)=1-16=-15 < 0 \quad \Longrightarrow \quad x=2 }`

`\large\displaystyle\text{$\begin{gathered}\sf \pmb{3) \ 6x^3+7x^2-9x+2=0 } \end{gathered}$}`

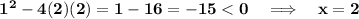
Synthetic division is used since the equation is of the third degree. The divisors of 2 are 1, -1, 2, -2. So:

| 6 7 9 2

-2 | -12 10 -2

6 -5 1 0

So the factorization is (x+2)(6x²-5x+1)=0 . The quadratic equation is solved by the general formula:

`\bf{ x_(2, 3)&=(5\pm √((5)^2-4(6)(1)))/(2(6))=(5\pm √(25-24))/(12)=(5\pm 1)/(12) }}`

`\large\displaystyle\text{$\begin{gathered}\sf \begin{matrix} x_1=-2&\ \ \ \ \ \ x_(2)=(6)/(12) \qquad &\ \ \ x_3=(4)/(12)\\ &\ \ \ x_2=(1)/(2) \qquad &x_3=(1)/(3) \end{matrix} \end{gathered}$}`