Question

Yeah you have a square garage 366 ft.² floor space she recently built in addition to the garage is the square but I have 50% more force base what is the length of one side of the garage originally what is the length of one side of the garage now what was the percent increase in the length of one side

Answer 1

a) The original length of the garage is 19.13 feet.

b) The new length of the garage is 23.43 feet.

c) Percentage increase in the length of one side is 22.5%.

Explanation:

The original area of the garage = 366
`ft^(2)`

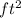
a) Area of a square = length x length (since it has equal length of sides)

=
`l^(2)`

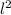
So that;

366 =
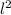
`l^(2)`

l =
`√(366)`

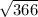
= 19.131

The original length of the garage is 19.13 feet.

b) 50% more force base = 50% x 366

= 0.5 x 366

= 183

The new area of the garage = 366 + 183

= 549
`ft^(2)`

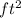
So that;

549 =
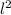
`l^(2)`

l =
`√(549)`

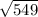
= 23.431

The new length of the garage is 23.43 feet.

c) Increase in the length of one side = 23.431 - 19.131

= 4.3 ft

Percentage increase in the length of one side =
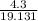`(4.3)/(19.131)` x 100%

= 22.48 x 100%

≅ 22.5%

Percentage increase in the length of one side is 22.5%.