Question

In ΔHIJ, \text{m}\angle H = (4x+1)^{\circ}m∠H=(4x+1) ∘ , \text{m}\angle I = (2x-6)^{\circ}m∠I=(2x−6) ∘ , and \text{m}\angle J = (6x-7)^{\circ}m∠J=(6x−7) ∘ . Find \text{m}\angle J.M∠J.

Answer 1

Given:

In ΔHIJ, m∠H=(4x+1)° , m∠I=(2x−6)°, and m∠J=(6x−7)° .

To find:

The m∠J.

Solution:

According to the angle sum property, the sum of all interior angles of a triangle is 180 degrees.

In ΔHIJ,

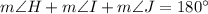`m\angle H+m\angle I+m\angle J=180^\circ` [Angle sum property]

`(4x+1)^\circ+(2x-6)^\circ+(6x-7)^\circ=180^\circ`

`(12x-12)^\circ=180^\circ`

`12x-12=180`

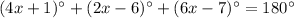
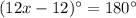
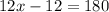
Add 12 on both sides.

`12x=180+12`

`12x=192`

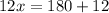
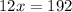
Divide both sides by 12.

`x=16`

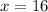
Now,

`m\angle J=(6x-7)^\circ`

`m\angle J=(6(16)-7)^\circ`

`m\angle J=(96-7)^\circ`

`m\angle J=89^\circ`

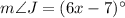
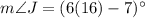
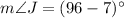
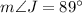
Therefore, the measure of angle J is 89 degrees.