Question

The field inside a running track is made up of a rectangle 84.39m (meters) long and 73m (meters) wide, together with a half-circle at each end. The running lanes are 9.76m (meters) wide all the way around. Question: What is the area of the running track that goes around the field? Explain or show your reasoning.

Answer 1

3886.53
`m^(2)`

Explanation:

The running track consist of two semicircles and a rectangle.

So that;

Diameter of the semicircles = width of the rectangle = 73 m

radius =
`(diameter)/(2)`

=
`(73)/(2)`

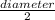
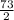
= 36.5 m

But the two semicircles form a circle, so that;

Circumference of a circle = 2
`\pi`r

Circumference of the circle formed by the semicircles = 2 x
`(22)/(7)` x 36.5

= 229.43 m

Thus,

length of the running track = circumference of the circle formed + length of the two sides of the rectangle

= 229.43 + 84.39 + 84.39

= 398.21 m

The length of the running track is 398.21 m.

Therefore;

Area of the running track = length x width

= 398.21 x 9.76

= 3886.5296

The area of the running track is 3886.53
`m^(2)`.