Question

A projectile is launched at an angle of 45 degrees with a velocity of 250 m/s. If air resistance is neglected, the magnitude of the horizontal velocity of the projectile at the time it reaches maximum altitude is equal to

Answer 1

The horizontal velocity of the projectile at the time it reaches maximum altitude approximately equal to 131.331 meters per second.

Step-by-step explanation:

From Mechanical Physics we understand that projectile motion is the combination of a horizontal motion at constant velocity and a vertical uniform accelerated motion due to gravity. Then, the horizontal velocity of the projectile (
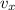`v_(x)`), measured in meters per second, remains constant during motion. That is:

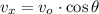`v_(x) = v_(o)\cdot \cos \theta` (Eq. 1)

Where:

`v_(o)` - Initial velocity of the projectile, measured in meters per second.

`\theta` - Launch angle above the horizontal, measured in sexagesimal degrees.

If we know that
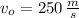`v_(o) = 250\,(m)/(s)` and
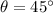`\theta = 45^(\circ)`, then horizontal velocity of the projectile at the time it reaches maximum altitude is:

`v_(x) = \left(250\,(m)/(s) \right)\cdot \cos 45^(\circ)`

`v_(x) \approx 131.331\,(m)/(s)`

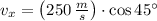
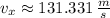
The horizontal velocity of the projectile at the time it reaches maximum altitude approximately equal to 131.331 meters per second.