Question

Using the information below, answer the next 3 questions: The percent of fat calories that a person in America consumes each day is normally distributed with a mean of about 36 and a standard deviation of about 10. Suppose that 16 individuals are randomly chosen. For the group of 16, find the probability that the average percent of fat calories consumed is more than thirty-five (Round to 3 decimal places)

Answer 1

Answer: 0.655

Explanation:

Let X be a random variable that represents percent of fat calories that a person in America consumes each day.

As per given , X is normally distributed with a mean
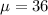`\mu=36` and a standard deviation
`\sigma=10`.

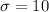Sample size : n= 16

The probability that the average percent of fat calories consumed is more than 35:

`P(\overline{X}>35)=P(\frac{\overline{X}-\mu}{(\sigma)/(√(n))}>(35-36)/((10)/(√(16))))\\\\=P(Z>(-1)/((10)/(4)))\ \ \ [Z=\frac{\overline{X}-\mu}{(\sigma)/(√(n))}]\\\\=P(Z>(-4)/(10))\\\\=P(Z>-0.4)\\\\=P(Z<0.4)\ \ \ [P(Z>-z)=P(Z<z)]\\\\=0.655\ \ \ [\text{By p-value table}]`

Hence, Required probability =0.655