Answer: $430.90
Explanation:
Given formula :
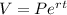 , where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest.
, where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest.
Given: P= $290 , r=2.2% = 0.022 [divide percent by 100 to remove percent sign '%']
Also, t=18 years
Now,
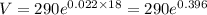

Hence, the amount of money in the account after 18 years. = $430.90