Question

You are given four tuning forks.The fork with the lowest frequency oscillates at 500 Hz. By striking two tuning forks at a time, you can produce the following beat frequencies, 1, 2, 3, 5, 7, and 8 Hz. What are the possible frequencies of the other three forks

Answer 1

Follows are the solution to this question:

Step-by-step explanation:

Least frequency
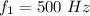`f_1=500 \ Hz` Its maximum beat frequency is 8 Hz from the specified condition. The highest frequency, thus
`f_4 =508 \ Hz`

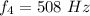
Now we calculate the value of frequency in Hz that are:

`from\ \ 1 Hz \ \ to\ \ 7 Hz:\\\\f_2= 501 \ Hz \ \ or \ \ 507 \ Hz\\\\ f_3 = 503 \ Hz \ \ or \ \ 505 Hz`

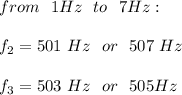
calculate the value from sets:

`set \ 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ set \ 2\\\\500, 501 ,503, ... 508 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 500, 505, 507,..508\\\\501 - 500 = 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 508-507=1\\\\503 - 501 = 2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 507-505=2\\\\`

`508 - 503 = 3 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 508-505=3\\\\508 - 501 = 7 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 507-500=7\\\\508 - 500 = 8 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 508-500=8\\\\`