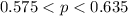Question

The Township Board of Meridian Township wants to know how much public support there is for raising property taxes to fix and maintain the roads in the township. They randomly surveyed Township residents and calculated a 90% confidence interval for the actual proportion of Meridian Township residents who are in favor of the tax increase to be (0.58, 0.63).

Answer 1

Complete Question

The Township Board of Meridian Township wants to know how much public support there is for raising property taxes to fix and maintain the roads in the township. They randomly surveyed Township residents and calculated a 90% confidence interval for the actual proportion of Meridian Township residents who are in favor of the tax increase to be (0.58, 0.63).

1. What is the sample proportion? Give the exact answer as a decimal.

2. Which of the following statements must be true?

A. If the sample size had instead been 960 residents, then the 90% confidence interval would be half as wide as the one stated above.

B. A 99% confidence interval calculated using the same survey data will include more plausible values for the population proportion.

C. If a different sample of 480 residents were to be selected, then there is a 90% chance that the new sample proportion will be between 0.57 and 0.62

3. What is the margin of error for this confidence interval? Give the exact answer as a decimal.

4. What is the standard error for this confidence interval? Round your answer to 4 decimal places.

5. What is the 95% confidence interval using the same survey data?

Answer:

1

`\^ p = 0.605`

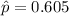
2

Correct option is B

3

`E =0.025`

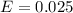
4

`SE = 0.0152`

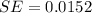
5

The 95% confidence interval is
`0.575<  p < 0.635`

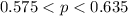
Explanation:

From the question we are told that the

The 90% confidence interval is (0.58, 0.63)

From the question we are told the confidence level is 90% , hence the level of significance is

`\alpha = (100 - 90 ) \%`

=>
`\alpha = 0.10`

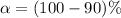
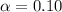
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  1.645`

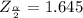
Generally the sample proportion is mathematically represented as

`\^ p = (0.63 + 0.58)/(2)`

=>
`\^ p = 0.605`

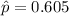
Generally the width of a confidence varies directly with the margin of error and this margin of error varies directly with the critical value which increases as the level of confidence increases

So if the confidence level is increased from 90 to 99 the critical value will increase which will increase the margin of error , which will increase the width of the confidence interval (and an increase in the width of confidence interval means that more plausible values for the population proportion will be included )

Therefore the correct option for question 2 is B

Generally the margin of error is mathematically represented as

`E =(0.63 - 0.58 )/(2)`

=>
`E =0.025`

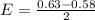
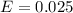
Generally the margin of error can also be mathematically represented as

`E = Z_{(\alpha )/(2) } * SE`

=>
`0.025 = 1.645 * SE`

=>
`SE = 0.0152`

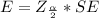
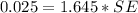
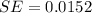
From the question we are told the confidence level is 95% , hence the level of significance is

`\alpha = (100 - 95 ) \%`

=>
`\alpha = 0.05`

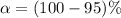
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  1.96`

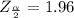
Generally the margin of error can also be mathematically represented as

`E = 1.96 * 0.0152`

=>
`E = 0.02979`

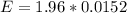
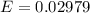
Generally 95% confidence interval is mathematically represented as

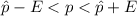
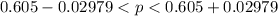
`\^ p -E <  p <  \^ p +E`

=>
`0.605  -0.02979 <  p < 0.605  +0.02979`

=>
`0.575<  p < 0.635`