Question

Which of the following equations is the perpendicular bisector of the line AB given:

A(3,1) & B(-3,6)
O y = 6/5x + 4
O y = 6/5x + 9/2
O y = 6/5x + 7/2
O y = -5/6x + 7/2

Answer 1

C. y = ⁶/5x + ⁷/2

Explanation:

First, find the slope of line AB that goes through A(3, 1) and B(-3, 6):

`slope(m) = (y_2 - y_1)/(x_2 - x_1) = (6 - 1)/(-3 - 3) = (5)/(-6)`.

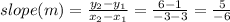Slope of line AB = -⅚.

The slope of the line that is a perpendicular bisector of line AB will be a negative reciprocal of the slope of line AB.

Thus:

Negative reciprocal of -⅚ = ⁶/5. (Reciprocal of ⅚, also the sign will change from positive to negative).

Next is to find the y-intercept, b, of the line.

To do this, you need to find the midpoint where the two lines intersect:

Therefore,

Midpoint (M) of AB, for A(3, 1) and B(-3, 6) is given as:

`M((x_1 + x_2)/(2), (y_1 + y_2)/(2))`

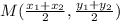
Let
`A(3, 1) = (x_1, y_1)`

`B(-3, 6) = (x_2, y_2)`

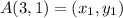
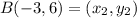
Thus:

`M((3 +(-3))/(2), (1 + 6)/(2))`

`M((0)/(2), (7)/(2))`

`M(0, (7)/(2))`

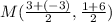
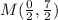
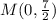
Substitute x = 0, y = ⁷/2, and m = ⁶/5 into y = mx + b and find the value of b.

⁷/2 = ⁶/5(0) + b

⁷/2 = b

b = ⁷/2

The slope (m) and the y-intercept, b, of the line we are looking for are ⁶/5 and ⁷/2, respectively.

Therefore, substitute m = ⁶/5 and b = ⁷/2 into y = mx + b.

y = ⁶/5x + ⁷/2

The equation that is the perpendicular bisector of the line AB is y = ⁶/5x + ⁷/2.