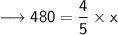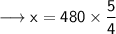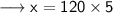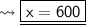Given that y is directly proportional to x.
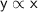
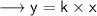

At first, we must find the value of k.
We have a relation given between 'x' and 'y' (that is, when 'x' is 75, 'y' is 60). We can call that Case - 1.
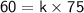
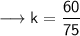
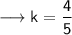

Now, we have to find 'x' when 'y' is 480. We can call that Case - 2.
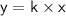
We are having the value of 'y' and 'k'.