Answer:
Find the first and second derivatives:

To find the stationary points (local minimum and maximum) set the first derivative to zero and solve for x:
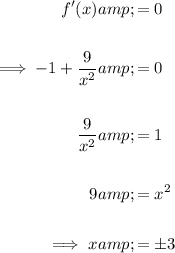
To determine the type of stationary points, input the found values of x into the second derivative.
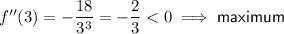

Finally, to find the y-values of the stationary points, input the found values of x into the original function:
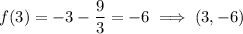
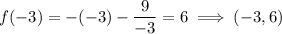
Therefore:
