Answer:
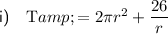
ii) radius = 1.27 cm (3 sf)
height = 2.55 cm (3 sf)
Explanation:

Given volume = 13 cm³, rewrite the equation making h the subject:
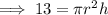
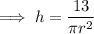
Substitute found expression for h into the Surface Area equation to find the expression for the total surface area, T:

To find the radius of the minimum surface area, differentiate T with respect to r:
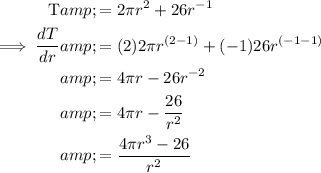
Set it to zero, and solve for r:
![\begin{aligned}(dT)/(dr) & = 0 \\\implies (4 \pi r^3-26)/(r^2) & = 0 \\\impliles 4 \pi r^3-26 & = 0 \\4 \pi r^3 & = 26 \\r^3 & = (13)/(2 \pi) \\r & = \sqrt[3]{(13)/(2 \pi)} \end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/lqomidsnacaget2kqxfrzu42k4rlmz61nv.png)
To find the height, substitute the found value of r into the equation for height (found previously):
![\begin{aligned}h & =(13)/(\pi r^2) \\\implies h & =\frac{13}{\pi \left(\sqrt[3]{(13)/(2 \pi)}\right)^2} \\& =2.548499134\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/yth2xj16wdpos2r117kd8mwpo7qk43mpwt.png)
Therefore,
- radius = 1.274249567... = 1.27 cm (3 sf)
- height = 2.548499134... = 2.55 cm (3 sf)