Answer:
Given:
As the exponent of Sample A is negative, this means that the mass of Sample A is smaller than that of Sample B.
Therefore, to find the proportional relationship between the samples, divide the mass of the larger sample (B) by the mass of the smaller sample (A):
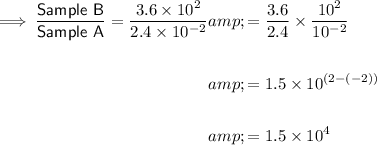
To convert the scientific notation
 to a decimal, move the decimal point to the right 4 places:
to a decimal, move the decimal point to the right 4 places:
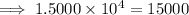
(If the exponent is positive, move the decimal point to the right. If the exponent is negative, move the decimal point to the left. The number of places to move the decimal point is the numerical value of the exponent).
Therefore, the mass of sample B is 15,000 times the mass of sample A, so Narissa is correct.