Question

Solve the system of equations -8x-6y=58 and x-y=9

Answer 1

`(-(2)/(7),-(65)/(7) )`

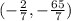
Explanation:

By steps in the image:

Step 1:

To eliminate, you need one of the coefficients to be the same in both equations. We will use the term "-6x" found in the first equation.

To get this, multiply the entire second equation by 6 and simplify using the distributive property. The new equation is:

`6x-6y=54`

Step 2:

Now you need to subtract the first equation and the new version of the second equation. By doing this, the "-6x" in both equations will cancel each other out.

Step 3:

Solve for x in the given equation by:

1. Dividing both sides by -14
2. Simplify the value of x by dividing top and bottom by 2

Step 4:

Solve for y by:

1. Substitute the value of x into the second equation
2. Multiply both sides of the equation by 7
3. Add 2 to both sides of the equation
4. Divide both sides of the equation by -7

Solution:

`(-(2)/(7),-(65)/(7) )`

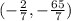
:Done