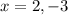How many different roots does the polynomial function have y = (x-2)(x+3)^2 have

Question

asked Jul 7, 2023 49.5k views

1 Answer

Haffax · Answer 1 · 2023-07-11T13:55:56+0000

Answer:

x=2,-3

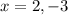
Explanation:

Set
(x-2)(x+3)^2 equal to
.

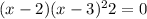
(x-2)(x-3)^22=0

Solve for
.

If any individual factor on the left side of the equation is equal to
, the entire expression will be equal to
.

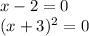
$x-2=0\\(x+3)^2=0$

Set the first factor equal to
and solve.

Set the first factor equal to
.

x-2=0

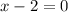
Add
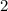to both sides of the equation.

x=2

Set the next factor equal to
and solve.

Set the next factor equal to
.

(x+3)^2=0

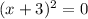
Set the
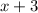x+3 equal to

x+3=0

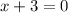
Subtract
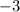from both sides of the equation.

x=-3

The final solution is all the values that make
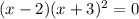(x-2)(x+3)^2=0 true.

x=2,-3