Answer:
 , assuming that the rollercoaster is not attached to the track.
, assuming that the rollercoaster is not attached to the track.
Step-by-step explanation:
Let
 denote the radius of the loop. The height of the top of the loop would be
denote the radius of the loop. The height of the top of the loop would be
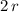 .
.
Let
 denote the acceleration of the rollercoaster. At any position in the loop, if the speed of the rollercoaster is
denote the acceleration of the rollercoaster. At any position in the loop, if the speed of the rollercoaster is
 , the (centripetal) acceleration of the rollercoaster would be:
, the (centripetal) acceleration of the rollercoaster would be:
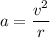 .
.
Let
 denote the mass of the rollercoaster. The net force on the rollercoaster would then be:
denote the mass of the rollercoaster. The net force on the rollercoaster would then be:
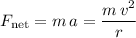 .
.
The rollercoaster would stay on the track (and goes around the loop without falling off) only if the normal force
 between the track and the rollercoaster is non-negative. In other words: it is necessary that
between the track and the rollercoaster is non-negative. In other words: it is necessary that
 for the rollercoaster to stay on the track.
for the rollercoaster to stay on the track.
At the top of the loop,
 and the weight of the rollercoaster
and the weight of the rollercoaster
 are in the same direction as the centripetal acceleration (downwards towards the center of the loop.) Hence:
are in the same direction as the centripetal acceleration (downwards towards the center of the loop.) Hence:
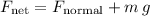 .
.
Let
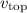 denote the speed of the rollercoaster at the top of the loop.
denote the speed of the rollercoaster at the top of the loop.
 .
.
If
 at the top of the loop, then:
at the top of the loop, then:
 .
.
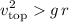 .
.
At the same time, by the conservation of energy, the sum of the kinetic energy
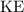 and gravitational potential energy
and gravitational potential energy
 of the rollercoaster should stay the same during the entire ride. Assuming that
of the rollercoaster should stay the same during the entire ride. Assuming that
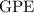 is
is
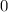 at the bottom of the loop:
at the bottom of the loop:
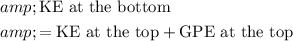 .
.
Let
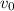 denote the speed of the rollercoaster at the bottom of the loop.
denote the speed of the rollercoaster at the bottom of the loop.
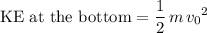 .
.
The speed of the rollercoaster at the top of the loop
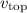 is at least
is at least
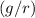 . Therefore:
. Therefore:
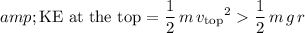 .
.
Since the height of the loop is
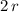 , the
, the
 of the rollercoaster at the top of the loop would be:
of the rollercoaster at the top of the loop would be:
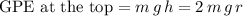 .
.
Thus:
 .
.
In other words:
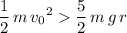 .
.
Rearrange and simplify to obtain a bound on
 :
:
 .
.
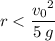 .
.
Given that
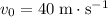 and
and
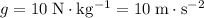 :
:
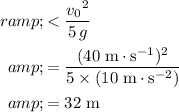 .
.
Hence, the radius of this loop is at most
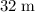 , such that the height of the top of this loop is at most
, such that the height of the top of this loop is at most
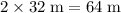 .
.