Answer:
The quotient is 6v³ + 2v² + 5v - 2
Explanation:
To solve using the synthetic Division
1. Arrange the variable according to its powers from greatest to smallest
2. Equate the divisor by 0 to find the value of the variable
3. Use the coefficients of the terms with it to find the quotient
Let us do that
∵ The dividend is

→ Arrange the terms from greatest power to the smallest power
∴ The dividend is
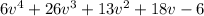
∵ The divisor is v + 4
→ Equate it by 0 to find v
∵ v + 4 = 0
→ Subtract 4 from both sides
∴ v + 4 - 4 = 0 - 4
∴ v = -4
→ Now use the coefficient of the terms with it
-4 → 6 26 13 18 -8
-------------------------------------- Multiply 6 by -4 and put the answer under 26
6 -24 13 18 -8
-------------------------------------- Add 26 and -24
6 2 13 18 -8
-------------------------------------- Multiply 2 by -4 and put the answer under 13
6 2 -8 18 -8
-------------------------------------- Add 13 and -8
6 2 5 18 -8
-------------------------------------- Multiply 5 by -4 and put the answer under 18
6 2 5 -20 -8
-------------------------------------- Add 18 and -20
6 2 5 -2 -8
-------------------------------------- Multiply -2 by -4 and put the answer under -8
6 2 5 -2 8
-------------------------------------- Add -8 and 8
6 2 5 -2 0
- The coefficients of the terms of the quotients are 6, 2, 5, -2
- The degree of the quotient is less than the degree of the dividend by 1
- The power of the greatest term of the quotient is v³
∴ The quotient is 6v³ + 2v² + 5v - 2