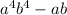Question

I’m literally so dumb omg

Answer 1

The expression not equivalent to a³b³ is a^4b^4 - ab

Explanation:

Answer 2

The expression NOT equivalent to a³b³ is
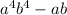`a^(4)b^(4)-ab` ⇒ B

Explanation:

Let us revise some rules of exponents

`a^(m)*a^(n)=a^(m+n)`

`(a^(m))/(a^(n))=a^(m-n)`

`(a^(m))^(n)=a^(mn)`

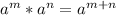
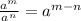
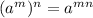
let us solve the question

∵ (a²b)(b²a) = a² × a × b × b²

∵ a² × a × b × b² =
`a^(2+1)` ×
`b^(2+1)`

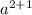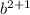
∴ a² × a × b × b² = a³ × b³

∴ (a²b)(b²a) = a³b³

∵
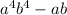`a^(4)b^(4)-ab` have mo multiplication or division operations

∴ We can not add the powers or subtract them

∴
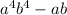`a^(4)b^(4)-ab` ≠ a³b³

∴ The expression NOT equivalent to a³b³ is
`a^(4)b^(4)-ab`