Answer:
AB = 12 in
Explanation:
Theorem
When a secant segment and a tangent segment meet at an exterior point, the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
Secant: a straight line that intersects a circle at two points.
Tangent: a straight line that touches a circle at only one point.
Given:
- Secant segment = BD
- External secant segment = BC
- Tangent segment = AB
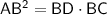
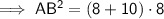
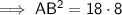
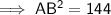
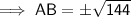
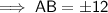
As distance is positive, AB = 12 in