Given:
The function is
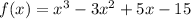
To find:
The root of the function from the given possible roots.
Solution:
We have,
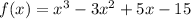
At x=-3,
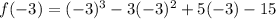
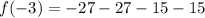
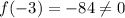
At x=-1,
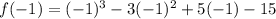
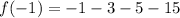
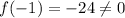
At x=1,
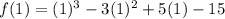
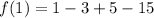
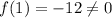
At x=3,
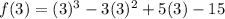
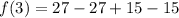
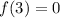
Since, the value of given function is 0 at only x=3, therefore 3 is a root of given function.
Hence, the correct option is D.