Question

Which of the following possible rational roots is a root of the function f(x)=x^3-3x^2+5x-15? *

5 points
-3
-1
1
3

Answer 1

Given:

The function is

`f(x)=x^3-3x^2+5x-15`

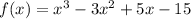
To find:

The root of the function from the given possible roots.

Solution:

We have,

`f(x)=x^3-3x^2+5x-15`

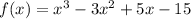
At x=-3,

`f(-3)=(-3)^3-3(-3)^2+5(-3)-15`

`f(-3)=-27-27-15-15`

`f(-3)=-84\\eq 0`

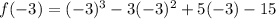
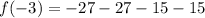
At x=-1,

`f(-1)=(-1)^3-3(-1)^2+5(-1)-15`

`f(-1)=-1-3-5-15`

`f(-1)=-24\\eq 0`

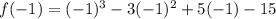
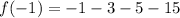
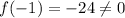
At x=1,

`f(1)=(1)^3-3(1)^2+5(1)-15`

`f(1)=1-3+5-15`

`f(1)=-12\\eq 0`

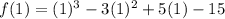
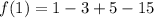
At x=3,

`f(3)=(3)^3-3(3)^2+5(3)-15`

`f(3)=27-27+15-15`

`f(3)=0`

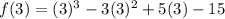
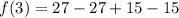
Since, the value of given function is 0 at only x=3, therefore 3 is a root of given function.

Hence, the correct option is D.