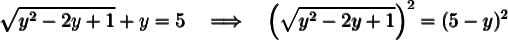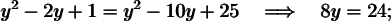The coefficient matrix associated with the system is constructed and the columns and rows are reduced.
![\left ( \begin{array}ccc 5 & -3 &-1 &1\\ 1 & 4 & -6 &-1\\ 2 & 3 & 4 & 9 \end{array} \right ) \begin{array}{c} \xrightarrow[\textup{F}_3- 2\textup{F}_2]{\textup{F}_1 - 5\textup{F}_2} \end{array} \left ( \begin{array}c 0 & -23& 29 &6\\ 1 & 4& -6 &-1\\ 0 & -5 &16 & 11 \end{array} \right )\\ \ \\ \ \\ \begin{array}{c} \xrightarrow[]{23\textup{F}_3 - 5\textup{F}_1} \end{array} \left ( \begin{array}ccc 0 & -23& 29 &6\\ 1 & 4& -6 &-1\\ 0 & 0 & 223 & 223 \end{array} \right )](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/sxaokmo6f03wfoon5qrw.png)
So, z=1. Translating the last matrix to the associated system of equations, we have that x=1, y=1, since:
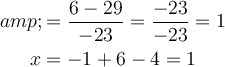

Clear an unknown in the first equation and substitute the resulting expression in the second. Next, the quadratic equation is solved.
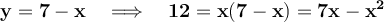
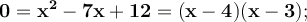
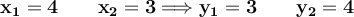
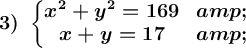
Clear an unknown in the first equation and substitute the resulting expression in the second. Next, the quadratic equation is solved.
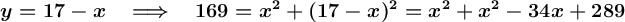
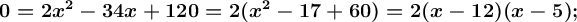

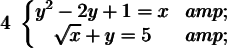
Substitute the expression that represents x into the second equation. Then both sides of the equation are squared and solved.