Question

USING Pythagoras theorem find the formula of equilateral triangle.​

Answer 1

Answer with explanation is below~

Explanation:

We could easily obtain the formulae/formula of an equilateral triangle not only through Pythagoras Theorem, but also through Heron's formula.

INTRODUCTION:

What's equilateral triangle?

• It's an triangle, whose all sides're of equal measurement.

What's Heron Formula?

• It's just a formula actually,take an example:Let,a,b and c denotes the lengths of 3 sides of any triangle,then the area will be given as:

`\boxed{\rm \: Area= √(s(s - a)(s - b)(s - c)) \: units ^(2)}`

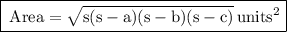
Where,

• s = (a+b+c)/2 {Half of the perimeter, basically}

What's Pythagoras' Theorem?

• It's actually like a formula but a theorem introduced by Pythagoras.

SOLVING:

Let,ABC an equilateral triangle of sides a.

Now:Draw a perpendicular straight line AM to the side BC(Name each part of triangle)

So it's clear that ∆AMB is a right angled triangle at M, BM = (1/2)BC = a/2.

Please note AM here represents the height of ∆ ABC.

• Let's use Pythagoras' theorem now.

`\boxed{\rm \: AM = √(AB^2-BM^2)}`

• AB = a
• BM = a/2

`\rm \: AM = \sqrt{a {}^(2) - { \bigg( \cfrac{a}{2} \bigg) }^(2) }`

`\rm \: AM = 3 \: \cfrac{a {}^(2) }{4}`

`\rm \: AM = \cfrac{ √(3) }{2} \: a`

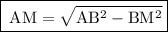
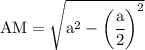
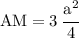
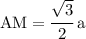
Now find the area of ∆ABC:

`\rm \triangle \: ABC = \cfrac{1}{2} * \: BC * A`

`\rm \: \triangle \: ABC = \cfrac{1}{2} * a * \cfrac{ √(3)}{4}a`

`\boxed{\rm\triangle \: ABC = \cfrac{ √(3 ) }{4} a {}^(2) \: units {}^(2)}`

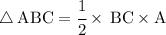
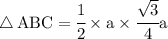
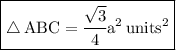
Hence,the formulae of equilateral triangle using Pythagoras' theorem is {√(3)/4} a^2

`\rule{225pt}{2pt}`

Extras:

Now let's find the area using Heron's Formula.

Solving:

Let each side of an equilateral triangle be a.

SO, then:

s = (3a/2)

We know that, (Heron's formula)

`\rm \: A = √(s(s - a)(s - b)(s - c))`

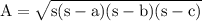
Now the area A :

`\rm AR(A)= \sqrt{ \cfrac{ 3a } 2 \bigg(\cfrac{ 3a }{2} - a \bigg)\bigg(\cfrac{ 3a }{2} - a \bigg)\bigg(\cfrac{ 3a }{2} - a \bigg)}`

`\rm AR(A)= \sqrt{ \cfrac{3a}{2} \bigg( \cfrac{a}{2} \bigg)\bigg( \cfrac{a}{2} \bigg)\bigg( \cfrac{a}{2} \bigg)}`

`\rm \boxed{ \rm AR(A)= \cfrac{ √( 3a)}{4} \: a {}^(2) \: \: units {}^(2)}`

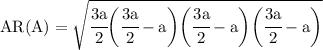
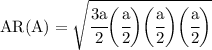
And voila! we're done!

I hope this helps! :)

[Figure of Equilateral triangle is attached, it denotes the triangle we need to draw while finding the formulae through Pythagoras' theorem. ]