Question

When playing many games, players must roll a pair of dice and find the sum of the two numbers rolled. With two dice, there are 11 possible sums ranging from 2 through 12. What is the probability that a player will roll a sum of 11 on his first roll of two dice? Express your answer as a common fraction.

Answer 1

`Probability = (1)/(18)`

Explanation:

Given

`Dice = 2`

Required

Probability of getting sum of 11

First, we need to list out the sample space;

Represent the first dice with S1 and the second with S2

`S_1 = \{1,2,3,4,5,6\}`

`S_2 = \{1,2,3,4,5,6\}`

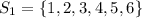
Represent the Sum of the outcome with S

So, the new sample space is the sum of outcome of S1 and S2

So, S is as follows:

`S = \{2,3,4,5,6,7,3,4,5,6,7,8,4,5,6,7,8,9,5,6,7,8,9,10,6,7,8,9,10,11,7,8,9,10,11,12\}`

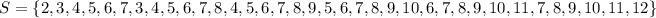
Represent the number of sample space with n(S)

`n(S) = 36`

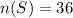
To determine the probability of outcome of 11, we need to list out the number of outcomes of 11.

Represent this with n(11)

From the sample space above,

`n(11) = 2`

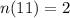
The required probability is then calculated as thus:

`Probability = (n(11))/(n(S))`

`Probability = (2)/(36)`

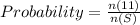
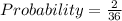
Simplify to the least term

`Probability = (1)/(18)`