Question

A lumber supplier sells 96-inch pieces of oak. Each piece must be within ¼ of an inch of 96 inches. Write and solve an inequality to show acceptable lengths.

Answer 1

`95 (3)/(4) \: inch \leqslant x \leqslant 96 (1)/(4) \: inch`

Explanation:

Given that a lumber supplier sells 96 inch Pieces of oak which must be within 1/4 of an inch.

This situation can be represented by the following absolute value inequality:

`|x \: - 96| \: \leqslant \: (1)/(4)`.

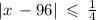The absolute value can be thought of as the size of something because length cannot be negative. The length must be no more than 1/4 away from 96.

To simplify this, pretend this is a standard equality, |x-96| = 1/4. 1/4 is the range of acceptable length, 96 is the median of the range, and x is the size of the wood.

First apply the rule |x| = y → x =
`\pm`y

|x-96| = 1/4

x - 96 =
`\pm`1/4

x =
`96 \pm 1/4`

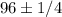
(These are just the minimum, and maximum sizes)

Now with a less than or equal to, the solutions are now everything included between these two values.

Therefore:

`96 - 1/4 \: \leqslant x`
`\leqslant \: 96 + 1/4`

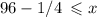
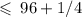
With less than inequalities, you must have the lower value on the left, and the higher value on the right.

If x represents the size of the pieces, then the acceptable lengths are represented by this following inequality:

`95 (3)/(4) \: inch \leqslant x \leqslant 96 (1)/(4) \: inch`

This is interpreted as x (being the size of the oak) is greater than or equal to 95 3/4, and less than or equal to 96 1/4 in inches.