Question

You are putting in a walkway around a tomato garden that has

dimensions of 14 feet x 8 feet. The width of the walkway needs to be
the same around each side of the garden. The total area of the
garden and the walkway needs to be 315 square feet.

Answer 1

The garden is 14ft by 8ft.

The width of the walkway needs to be the same around each side of the garden, let's suppose that the width is X.

Then the area of the garden plus the walkway will be:

(14ft + X) by (8ft + X).

And we want that the total area of the garden and the walkway must be equal to 315 ft^2. Then we must solve the equation:

(14ft + X)*(8ft + X) = 315ft^2

Let's solve this for X.

112ft^2 + 14ft*X + 8ft*X + X^2 = 315ft^2

Let's move al the terms to the same side:

X^2 + (14ft + 8ft)*X + 112ft^2 - 315ft^2 = 0

X^2 + 22ft*X - 203ft^2 = 0.

Now to solve this we can use Bhaskara's equation:

`X = (-22ft +- √((22ft)^2 - 4*1*(203ft^)) )/(2) = (-22ft +-36ft)/(2)`

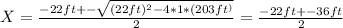
Then we have two solutions:

X = (-22ft - 36ft)/2 = -29ft

This solution is negative, and X represents a width, so must be positive, then we can discard this solution.

X = (-22ft + 36ft)/2 = 7ft

Then we can conclude that the width of the walkway must be 7ft.