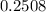Question

Según datos de una empresa aseguradora de vehículos, dos de cada cinco accidentes son provocados por conductores en estado de ebriedad, ¿cuál es la probabilidad de que tres de nueve accidentes seleccionados al azar hayan sido ocasionados por conductores ebrios?

Answer 1

La probabilidad es
`0.2508`

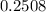
Explanation:

Sabemos que según datos de una empresa aseguradora de vehículos, dos de cada cinco accidentes son provocados por conductores en estado de ebriedad. Entonces, si definimos el evento

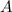`A` : ''Accidente provocado por un conductor en estado de ebriedad''

La probabilidad de este evento es

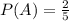`P(A)=(2)/(5)` (dato del problema)

Por lo tanto, en cada accidente que ocurre, la probabilidad de que ocurra el evento
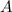`A` es
`(2)/(5)` .

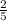Ahora bien, si suponemos cada uno de estos accidentes independientes y con probabilidad de ocurrencia ''p'' constante a lo largo del tiempo, estamos ante la presencia de un proceso Bernoulli.

Dado un proceso de Bernoulli, definimos la variable aleatoria discreta ''
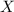`X`'' como el número de éxitos del proceso Bernoulli para un número fijo de ensayos.

En este caso vamos a definir

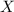`X` : ''Número de accidentes provocados por conductores en estado de ebriedad de un total de n accidentes''

Se dice que
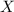`X` tiene distribución binomial de parámetros ''n'' y ''p''.

Lo denotamos
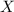`X` ~ Bi (n,p)

En nuestro ejercicio el valor de ''n'' es 9 (son los ensayos que fijamos) y el valor de ''p'' es
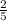`(2)/(5)` (definimos como ''éxito'' que el accidente sea provocado por un conductor en estado de ebriedad).

Ahora bien para calcular probabilidad vamos a utilizar la siguiente fórmula :

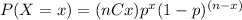`P(X=x)=(nCx)p^(x)(1-p)^((n-x))` (I)

''
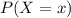`P(X=x)` '' es la probabilidad de que la variable aleatoria
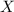`X` asuma el valor x. En particular, buscamos
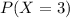`P(X=3)` que es la probabilidad de que de nueve accidentes (fijados), tres sean provocados por conductores en estado de ebriedad.

''
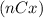`(nCx)` '' es el número combinatorio definido como

`nCx=(n!)/(x!(n-x)!)`

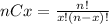
Reemplazando los datos en la ecuación (I) :

`P(X=3)=(9C3)((2)/(5))^(3)((3)/(5))^(6)=0.2508`

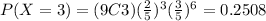
La probabilidad pedida es
`0.2508`