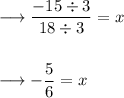Answer:
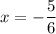
Explanation:
Given:
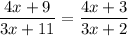
1. Cross-multiply
(4x + 9)(3x + 2) = (4x + 3)(3x + 11)
2. Distribute
⟶ (4x + 9)(3x + 2) = (4x + 3)(3x + 11)
⟶ 4x(3x) + 4x(2) + 9(3x) + 9(2) = 4x(3x) + 4x(11) + 3(3x) + 3(11)
⟶ 12x² + 8x + 27x + 18 = 12x² + 44x + 9x + 33
3. Combine like terms
⟶ 12x² + 8x + 27x + 18 = 12x² + 44x + 9x + 33
⟶ 12x² + 35x + 18 = 12x² + 53x + 33
4. Subtract 12x² from both sides
⟶ 12x² - 12x² + 35x + 18 = 12x² - 12x² + 53x +33
⟶ 35x + 18 = 53x + 33
5. Subtract 35x from both sides
⟶ 35x - 35x + 18 = 53x - 35x + 33
⟶ 18 = 18x + 33
6. Subtract 33 from both sides
⟶ 18 = 18x + 33
⟶ 18 - 33 = 18x + 33 - 33
⟶ -15 = 18x
7. Divide both sides by 18 to isolate the variable
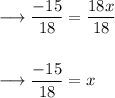
8. Reduce