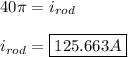Hi there!
We can begin by deriving the magnetic field strength for a circular loop at its center.
Using Biot-Savart's Law:
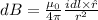
μ₀ = Permeability of free space (Tm/A)
dl = Differential length element
r = radius (m)
We can rather use 'ds' to represent a differential arc length since we are finding the magnetic field for a circular loop.
We must begin by dealing with the cross-product. Luckily, this derivation is simple since the radius vector is ALWAYS perpendicular to the path of integration along the loop's circumference. (ONLY if we are finding the field for the direct center.) Thus, since sin(90) = 1, we can get rid of the cross-product.
Therefore:
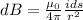
Now, we can integrate with respect to ds.
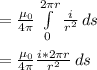
Simplify:
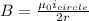
Now, for a straight conductor (assuming of infinite length), we know the magnetic field strength equation to be:
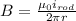
Set the two equal.

Cancel out '2', μ₀, and 'r':
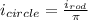
Plug in the given values and solve.