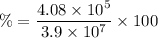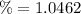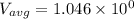Question

An atom of argon has a radius of and the average orbital speed of the electrons in it is about . Calculate the least possible uncertainty in a measurement of the speed of an electron in an atom of argon. Write your answer as a percentage of the average speed, and round it to significant digits.

Answer 1

Here is the full question:

An atom of argon has a radius of 71 .pm and the average orbital speed of the electrons in it is about 3.9 × 10⁷ m/s. Calculate the least possible uncertainty in a measurement of the speed of an electron in an atom of argon. Write your answer as a percentage of the average speed, and round it to significant digits.

Answer:

Step-by-step explanation:

From the above information:

The radius of an atom of argon = 71 .pm = 71 × 10⁻¹² m

The diameter of the atom of argon Δx =142 × 10⁻¹² m

According to Heisenberg's Uncertainty Principle,

`\Delta x. \Delta p_x \geq (h)/(2)`

`\Delta x. \Delta V \geq (h)/(4 \pi m_e)`

`\Delta V \geq (h)/(4 \pi m_e \Delta_x)`

`\Delta V \geq (6.634 * 10^(-34) \ J.s)/(4 \pi * 9.1 * 10^(-3) \ kg * 142 * 10^(-12) \ m)`

`\Delta V \geq (6.634 * 10^(-34) \ J.s)/(1.62382641 * 10^(-11) \ kg.m)`

`\Delta V \geq 4.08 * 10^5 \ m/s`

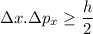
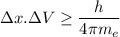
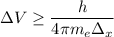
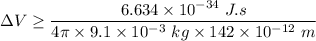
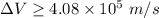
where; the average speed
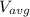`V_(avg)` = 3.9 10⁷ m/s

∴

The percentage of the average speed is expressed as a fraction of:

`\% = (4.08 * 10^5)/(3.9 * 10^7)* 100`

`\% =1.0462`

`V_(avg ) = 1.046 * 10^0`

`\mathbf{V_(avg )\simeq 1.0 \%}`