Question

A man and a woman agree to meet at a certain location about 12:30 PM. Suppose the man arrives at a time uniformly distributed between 12:15 and 12:45. Suppose the woman independently arrives at a time uniformly distributed between 12:00 and 1 PM. Find the probability that the man arrives first.

Answer 1

The probability that the man arrives first is 0.50.

Explanation:

Let X denote the arrival time of the man and Y denote the arrival time of the woman.

It is provided that:

`X\sim U[15,45]\\\\Y\sim U[0,60]`

The pdf of X an Y are:

`f_(X)(x)=(1)/(45-15)=(1)/(30);\ 15<X<45\\\\f_(Y)(y)=(1)/(60-0)=(1)/(60);\ 0<Y<60`

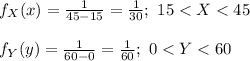
It is provided that X and Y are independent of each other.

Then the joint pdf of X and Y is:

`f_(XY)(x,y)=f_(X)(x)* f_(Y)(y)\\\\\Rightarrow f_(XY)(x,y)=(1)/(30)* (1)/(60)\\\\\Rightarrow f_(XY)(x,y)=(1)/(1800);\ 15<X<45,\ 0<Y<60`

Compute the probability that the man arrives first as follows:

`P(X<Y)=\int\limits^(45)_(15) {\int\limits^(60)_(x) {(1)/(1800)} \, dy } \,dx`

`=(1)/(1800)* \int\limits^(45)_(15) y|^(60)_(x) \,dx\\\\=(1)/(1800)* \int\limits^(45)_(15) {60-x} \,dx\\\\=(1)/(1800)* |60x-(x^(2))/(2)|^(45)_(15)\\\\=((1687.5-787.5))/(1800)\\\\=(900)/(1800)\\\\=(1)/(2)\\\\=0.50`

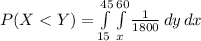
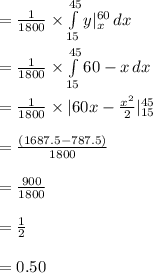
Thus, the probability that the man arrives first is 0.50.