Question

A rectangle has a height that is 5 inches less than the base. If the area of the rectangle is 57 inches square, what are the height and base of the rectangle?

Answer 1

The height and base of the rectangle are approximately 5.453 inches and 10.453 inches, respectively.

Explanation:

From Geometry we remember that area of a rectangle (
`A`), measured in square inches, is equal to:

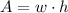`A = w \cdot h` (Eq. 1)

Where:

`w` - Width, measured in inches.

`h` - Height, measured in inches.

In addition, we get the following relationship from statement:

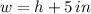`w = h+5\,in` (Eq. 2)

If we know that
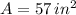`A = 57\,in^(2)`, then the height of the rectangle is:

`57\,in^(2) = (h+5\,in)\cdot h`

`h^(2)+5\cdot h -57 = 0`

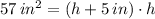
From Quadratic Formula we obtain the following roots:

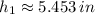`h_(1) \approx 5.453\,in` and
`h_(2)\approx -10.453\,in`

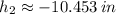
Only the first root offers a reasonable solution, as length has always positive values. Thus, the height of the rectangle is approximately 5.453 inches.

Now we calculate the width of the rectangle from (Eq. 1):

`w = (A)/(h)`

If we know that
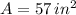`A = 57\,in^(2)` and
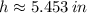`h \approx 5.453 \,in`, then the width of the rectangle is:

`w = (57\,in^(2))/(5.453\,in)`

`w \approx 10.453\,in`

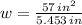
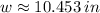
The height and base of the rectangle are approximately 5.453 inches and 10.453 inches, respectively.