Answer:
1,642.8 coulombs and 1.39*10²¹ electrons pass through any cross section the width of the wire.
Step-by-step explanation:
Electric current is the circulation of electric charges in an electric circuit, while electric current intensity (I) is the amount of electricity or electric charge (Q) that circulates through a circuit in unit time (t).
Then, the intensity of electric current is expressed as:
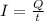
Where:
- I is the intensity expressed in Amps (A)
- Q is the electric charge expressed in Coulombs (C)
- t is the time expressed in seconds (s)
In this case:
- I= 7.4 A
- Q= ?
- t= 3.7 min= 222 s (being 1 min= 60 s)
Replacing:
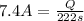
Solving:
Q= 7.4 A* 222 s
Q= 1,642.8 C
A Coulomb represents about 6.24*10¹⁸ electrons, so you can apply the following rule of three: if 1 C represents 6.24*10¹⁸ electrons, 222 C how many electrons does it represent?
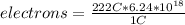
electrons= 1.39*10²¹
1,642.8 coulombs and 1.39*10²¹ electrons pass through any cross section the width of the wire.