Answer: 0.69727
Explanation:
Given: Sample size : n= 4
Number of defective calculators = 12
Number of non-defective calculators = 36
Total calculators = 12+36=48
Let X = Number of defective calculators.
The probability that a least one of the calculators is defective will be :
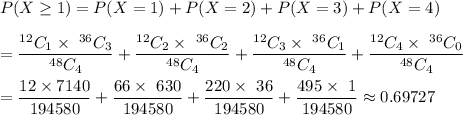
Hence, the required probability = 0.69727