Question

A sample of 4 different calculators is randomy selected from a group containing 12 that are defective and 36 that have no defects. What is the probability that a least one of the calculators is defective?

Answer 1

Answer: 0.69727

Explanation:

Given: Sample size : n= 4

Number of defective calculators = 12

Number of non-defective calculators = 36

Total calculators = 12+36=48

Let X = Number of defective calculators.

The probability that a least one of the calculators is defective will be :

`P(X\geq1)=P(X=1)+P(X=2)+P(X=3)+P(X=4)\\\\=(^(12)C_1*\ ^(36)C_(3))/(^(48)C_4)+(^(12)C_2*\ ^(36)C_(2))/(^(48)C_4)+(^(12)C_3*\ ^(36)C_(1))/(^(48)C_4)+(^(12)C_4*\ ^(36)C_(0))/(^(48)C_4)\\\\=(12*7140)/(194580)+(66*\ 630)/(194580)+(220*\ 36)/(194580)+(495*\ 1)/(194580)\approx0.69727`

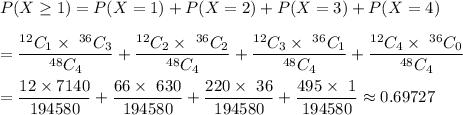
Hence, the required probability = 0.69727