Answer:
Approximately
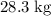 , assuming that the spring was pulled horizontally.
, assuming that the spring was pulled horizontally.
Step-by-step explanation:
Let
 denote the spring constant of this spring. Calculate the size of tension in this spring that corresponds to the
denote the spring constant of this spring. Calculate the size of tension in this spring that corresponds to the
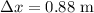 stretch:
stretch:
 .
.
(The negative sign is ignored.)
If the spring is pulled horizontally, then the tension that the spring exerts would be the only unbalanced force on this object. The net force n this object would be equal to the tension that the spring had exerted:
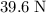 .
.
Newton's Second Law of motion suggests the following relation between the net force
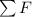 on the object, the mass
on the object, the mass
 of the object, and the acceleration
of the object, and the acceleration
 of the object:
of the object:
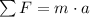 .
.
For this object,
 . It has been found that the net force on this object is
. It has been found that the net force on this object is
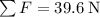 . Rearrange the original equation
. Rearrange the original equation
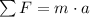 and solve for
and solve for
 , the mass of this object:
, the mass of this object:
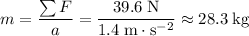 .
.
In other words (based on all these assumptions,) the mass of this object should be approximately
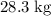 .
.