Question

An object is moving with an initial velocity of 20 m/s. If it is decelerating at 5 m/s2 how far does it travel before it stops

Answer 1

The object travels a distance of 40 meters before it stops.

Step-by-step explanation:

A body moves with constant acceleration motion or uniformly accelerated rectilinear motion (u.a.r.m) when the trajectory of the mobile is a straight line and its speed varies the same amount in each unit of time.

Torricelli's equation relates the speed to the space traveled by the body in u.a.r.m. To calculate the velocity of a body as a function of space, the expression is used:

`v^(2) =v0^(2) +2*a*d`

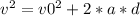
Where :

• v: final velocity (m/s)
• v0: initial velocity (m/s)
• a: acceleration (m/s²)
• d: space traveled by the body (m)

In this case:

• v: 0 m/s because the object stops
• v0: 20 m/s
• a: - 5 m/s² because the object is decelerating
• d: ?

Replacing:

`(0(m)/(s) )^(2) =(20 (m)/(s) )^(2) +2*(-5(m)/(s^(2) )) *d`

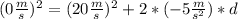
Solving:

`0(m^(2) )/(s^(2) ) =400 (m^(2) )/(s^(2) ) -10(m)/(s^(2) ) *d`

`0(m^(2) )/(s^(2) ) -400 (m^(2) )/(s^(2) ) = -10(m)/(s^(2) ) *d`

`-400 (m^(2) )/(s^(2) ) = -10(m)/(s^(2) ) *d`

`( -400 (m^(2) )/(s^(2) ))/( -10(m)/(s^(2) )) = d`

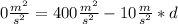
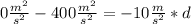
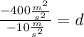
40 m= d

The object travels a distance of 40 meters before it stops.