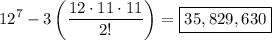Question

Consider a melody to be 7 notes from a single piano octave, where 2 of the notes are white key notes and 5 are black key notes. Notes can be repeated. How many melodies are possible if the 5 black notes cannot all be "adjacent" in the melody? Adjacent in this context meaning not adjacent on the piano keyboard but occurring without white notes between them. For example, while the pattern WWBBBBB is not allowed, the pattern WBWBBBB is.

Answer 1

35,829,630 melodies

Explanation:

There are 12 half-steps in an octave and therefore
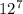`12^7` arrangements of 7 notes if there were no stipulations.

Using complimentary counting, subtract the inadmissible arrangements from
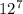`12^7` to get the number of admissible arrangements.

`\displaystyle \_\_ \:B_1\_\_ \:B_2\_\_ \:B_3\_\_ \:B_4\_\_ \:B_5\_\_`

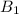`B_1` can be any note, giving us 12 options. Whatever note we choose,
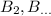`B_2, B_(...)` must match it, yielding
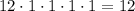`12\cdot 1\cdot 1\cdot 1\cdot 1=12`. For the remaining two white key notes,
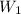`W_1` and
`W_2`, we have 11 options for each (they can be anything but the note we chose for the black keys).

There are three possible arrangements of white key groups and black key groups that are inadmissible:

`WWBBBBB\\WBBBBBW\\BBBBBWW`

White key notes can be different, so a distinct arrangement of them will be considered a distinct melody. With 11 notes to choose from per white key, the number of ways to inadmissibly arrange the white keys is
`\displaystyle(11\cdot 11)/(2!)`.

Therefore, the number of admissible arrangements is:

`\displaystyle 12^7-3\left((12\cdot 11\cdot 11)/(2!)\right)=\boxed{35,829,630}`