Question

Determine whether a statement is True or False. If it is False, provide an explanation or give an example:

Answer 1

Complete Question:

Determine whether the statement is true or false. If it is false, provide an explanation or give an example.

If f is decreasing on [a,b] then the minimum value of f(x) on [a,b] is f(a)?

Answer:

False

Explanation:

Given

[a,b]

Where f(x) is decreasing

Required

Is the minimum f(a)?

This statement is false and it is proved using the following illustration

Take f(x) to be

`f(x) = -2x`

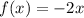
The above represents a decreasing function because:

f(x) decreases as x increases

Having said that:

Assume [a,b] is:

`[a,b] = [2,5]`

Substitute the value of a i.e. 2 for x in f(x)

`f(2) = -2 * 2`

`f(2) = -4`

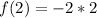
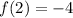
Substitute the value of b i.e. 5 for x in f(x)

`f(5) = -2 * 5`

`f(5) = -10`

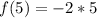
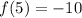
Notice that f(b) < f(a) i.e. -10 is less than -4

Hence:

f(x) is minimum at f(b)

Conclusively, the statement is false