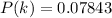Question

You have two chances to draw from a normal pack of 52 playing cards. What is the probability of drawing an ace on the second attempt if the first card (which you did NOT put back in the pack) was not an ace

Answer 1

The probability is
`P(k) =0.07843`

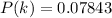
Explanation:

From the question we are told that

The total number of cards is n = 52

Generally the number of ace in a standard deck of cards is k = 4

Generally the the first card drawn is not an ace so the remaining number of ace after the first card is drawn is k = 4

also the remaining total number of cards after the first card is drawn is

N = n- 1

=> N = 52 - 1

=> N = 51

Generally the probability of drawing an ace on the second attempt if the first card (which you did NOT put back in the pack) was not an ace is mathematically represented as

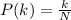
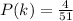
`P(k) =(k)/(N)`

=>
`P(k) =(4)/(51)`

=>
`P(k) =0.07843`