Question

Suppose that a sample of n students at the same university​ (instead of n​) determines that ​% of the sample use the web browser. At the level of​ significance, is there evidence that the market share for the web browser at the university is greater than the worldwide market share of ​%?

Answer 1

Complete Question

The worldwide market share for a web browser was 20.5​% in a recent month. Suppose that a sample of 200 random students at a certain university finds that 50 use the browser.

At the 0.05 level of​ significance, is there evidence that the market share for the web browser at the university is greater than the worldwide market share of 20.5​%?

Answer:

The decision rule is

Fail to reject the null hypothesis

The conclusion is

There is no sufficient evidence to show that the market share for the web browser at the university is greater than the worldwide market share of 20.5 ​%?

Explanation:

From the question we are told that

The population proportion is
`p = 0.205`

The sample size is n = 200

The number that uses the browser is k = 50

The level of significance is
`\alpha = 0.05`

Generally the sample proportion is mathematically represented as

`\^ p = (50)/(200)`

=>
`\^ p = 0.250`

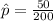
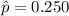
The null hypothesis is
`H_o : p = 0.205`

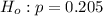
The alternative hypothesis is
`H_a : p > 0.205`

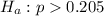
Generally the test statistics is mathematically represented as

`z = \frac{ \^ p - p }{ \sqrt{ ( p (1 - p ))/( n) } }`

=>
`z = \frac{ 0.250 - 0.205 }{ \sqrt{ ( 0.205 (1 - 0.205 ))/( 200) } }`

=>
`z = 1.5764`

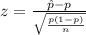
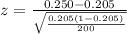
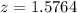
Generally the area under
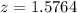`z = 1.5764` to the right is

`p-value = P( Z > 1.5764 ) = 0.057467`

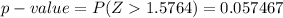
From the value we obtained we can see that the
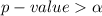`p-value > \alpha` hence

The decision rule is

Fail to reject the null hypothesis

The conclusion is

There is no sufficient evidence to show that the market share for the web browser at the university is greater than the worldwide market share of 20.5 ​%?