Given:
A new four way intersection is being constructed in New York Hyde park through point P(-3,-15).
Equation of line of one road :
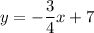 .
.
New road that will run perpendicular to the first road
To find:
The equation of line for the new road.
Solution:
The slope intercept form of a line is

where, m is slope and b is y-intercept.
We have,
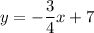
Slope of this line is
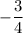 and y-intercept is 7.
and y-intercept is 7.
Product of slopes of two perpendicular line is -1.
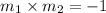
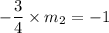
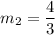
The point slope form of a line is

where, m is slope.
The slope of new line is
 and it passes through P(-3,-15). So, the equation of line of new road is
and it passes through P(-3,-15). So, the equation of line of new road is
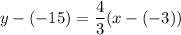
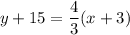
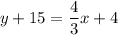
Subtract 15 from both sides.

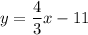
Therefore, the equation of the line representing the new road is
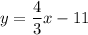 .
.