Question

A test for ovarian cancer has a 4 percent rate of false positives and a 1 percent rate of false negatives. On average, 1 in every 2,000 American women over age 35 actually has ovarian cancer. If a woman over 35 tests positive, what is the probability that she actually has cancer

Answer 1

The probability that a woman over 35 actually has cancer given that she tests positive is 0.012.

Explanation:

The information provided is:

P (+ | X') = 0.04

P (- | X) = 0.01

P (X) = 0.0005

Compute the value of P (+ | X) as follows:

P (+ | X) = 1 - P (- | X)

= 1 - 0.01

= 0.99

Compute the value of P (+) as follows:

P (+) = P (+ | X) × P (X) + P (+ | X') × P (X')

`=(0.99* 0.0005)+(0.04* (1-0.0005))\\\\=0.000495+0.03998\\\\=0.040475\\\\\approx 0.0405`

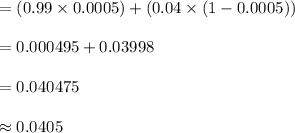
Compute the probability that a woman over 35 actually has cancer given that she tests positive as follows:

`P(X|+)=(P(+|X)P(X))/(P(+))`

`=(0.99* 0.0005)/(0.0405)\\\\=0.0122222\\\\\approx 0.012`

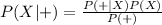
Thus, the probability that a woman over 35 actually has cancer given that she tests positive is 0.012.