Question

The 95% confidence interval for a certain proportion p is from 0.23 to 0.63. We conducted a hypothesis test for p. The null hypothesis is H0:p=a . The alternative hypothesis is Ha:p≠a. What is the mean for the all possible values of a which would not be rejected as plausible values of the population proportion at a 5% significance level? The mean for the all possible values of a which would not be rejected as plausible values of the population proportion at a 5% significance level is .

Answer 1

The answer is "0.43"

Explanation:

Population proportion normal distribution is suggested as following:

Confidence Interval =
`P \pm Z * \sqrt{(P * (1 -p))/(n) }`

Confidence Interval =
`P \pm E`

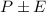
Bottom bound
`= P-E = 0.23`

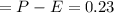
Lower bound
`= P + E = 0.63`

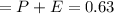
Through connecting additional formulas, we're getting,

`\to 2P = 0.23+0.63\\\\\to 2P = 0.86\\\\\to P= (0.86)/(2)\\\\`

`= 0.43`

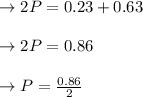
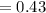
The average with all attribute outcomes a whereby the demographic proportion at 5 % isn't dismissed as plausible values is 0.43.