Answer:
Mike has 13 dimes and 12 nickels.
Explanation:
Topic: System of Equations
Let: d = # of dimes
n = # of nickels
System of equations:
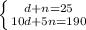
The method I am using today is the Substitution Method.
Substitution Method
- Solve for one variable in 1 equation
- plug in the other side into the other equation
- Solve for the other variable
- Plug-in that variable into the other equation to receive the second variable
Step 1: Solve for d
I am going to solve for one variable, d, from the top equation
Isolate d
Step 2: Plug in the value for d in the other equation
Now, we plug in d = 25 - n for 10d
- 10d + 5n = 190
- 10(25 - n) + 5n = 190
- 250 - 10n + 5n = 190
Step 3: Solve for n
Now we have an equation with 1 variable, we can solve for that variable.
- 250 - 10n + 5n = 190
- 250 - 5n = 190
- -5n = -60
- -n = -12
- n = 12
Step 4: Solve for d
Now, all we have to do is plug in "n" into an original equation
- d + n = 25
- d + 12 = 25
- d = 13
Mike has 13 dimes and 12 nickels.
-Chetan K