Question

Mike has a total of 25 dimes and nickels. If the total value of the coins is $1.90 how many of each coin does he have? ​

Answer 1

12 nickels and 13 dimes

Explanation:

d = # of dimes

n = # of nickels

Set up a System of Equations as follows:

d + n = 25

.10d + .05n = 1.90

now solve for 'd' or 'n' and use Substitution:

d = 25-n

.10(25-n) + .05n = 1.90

2.5 - .10n + .05n = 1.90

-.10n + .05n = -0.6

-.05n = -0.6

n = -0.6/-.05

n = 12

d + 12 = 25

d = 13

Check: 12(.05) + 13(.10) should equal 1.90

0.60 + 1.30 = 1.90

1.90 = 1.90

Answer 2

Mike has 13 dimes and 12 nickels.

Explanation:

Topic: System of Equations

Let: d = # of dimes

n = # of nickels

System of equations:

`\left \{{d + n= 25} \atop {10d + 5n = 190}} \right.`

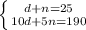
The method I am using today is the Substitution Method.

Substitution Method

• Solve for one variable in 1 equation
• plug in the other side into the other equation
• Solve for the other variable
• Plug-in that variable into the other equation to receive the second variable

Step 1: Solve for d

I am going to solve for one variable, d, from the top equation

Isolate d

• d + n = 25
• d = 25 - n

Step 2: Plug in the value for d in the other equation

Now, we plug in d = 25 - n for 10d

• 10d + 5n = 190
• 10(25 - n) + 5n = 190
• 250 - 10n + 5n = 190

Step 3: Solve for n

Now we have an equation with 1 variable, we can solve for that variable.

• 250 - 10n + 5n = 190
• 250 - 5n = 190
• -5n = -60
• -n = -12
• n = 12

Step 4: Solve for d

Now, all we have to do is plug in "n" into an original equation

• d + n = 25
• d + 12 = 25
• d = 13

Mike has 13 dimes and 12 nickels.

-Chetan K