80 adult tickets were sold that day.
This is a two equation problem.
First, let:
a = adult tickets
c = child tickets
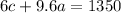
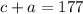
Now, solve for either variable (c or a). We're going to isolate "c" in the second equation and plug it into the first.
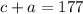
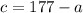
Plug it in:
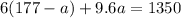
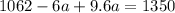
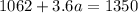
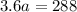
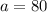
Now, plug in 80 for "a" in either of the equations to find "c."
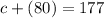
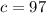
Rather than solving algebraically, as shown above, you can also graph the two equations, and wherever they intersect will be the solution.